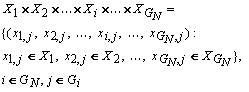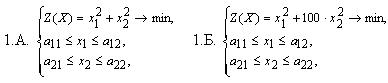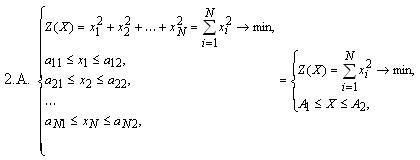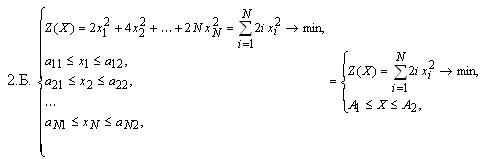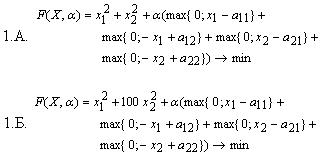Обоснование выбора метода оптимизации в задачах принятия решений по данным мониторинга образования

Исследованы методы решения оптимизационных задач, моделирующих процессы принятия решений на основе данных мониторинга образования. Предложена математическая модель принятия решений по данным мониторинга процессов информатизации образования.

Ключевые слова: выбор, метод оптимизации, принятие решений, мониторинг, образование, генетический алгоритм

ВВЕДЕНИЕ

Современное образование немыслимо без применения информационно-коммуникационных технологий, комплексное внедрение которых осуществляется в рамках информатизации образования. Качество процессов и результатов информатизации в значительной степени определяет и качество образования в целом. В связи с этим возникает необходимость существования схемы управления процессами информатизации образования, которые можно представить в виде последовательности этапов: исследование объектов (учебных заведений) и исследование предмета (процессов информатизации). Другими словами можно говорить о следующих этапах в схеме управления процессами информатизации образования: мониторинг, обработка данных, принятие решений субъектом управления, реализация управляющего воздействия. В литературе эти этапы представлены в разной степени детализации: наиболее подробно проработан этап реализации управляющего воздействия, в то время как этапы организации мониторинга, анализ данных мониторинга, а также выработка рекомендаций при поддержке принятия решений по управлению образованием представляются все еще недостаточно исследованными.

Отслеживание процессов информатизации и их влияния на качество образования необходимо для адекватного управления образованием [1] и подразумевает проведение различных видов мониторинга: мониторинг информационных образовательных ресурсов, мониторинг компетенций в области информационных технологий учащихся и преподавателей т.д. [2].

Целью мониторинга в системе образования является предоставление оперативной и полной информации для поддержки органов управления в принятии решений, направленных на повышение качества образования и эффективное расходование средств.

Принятие решений по данным мониторинга образования подразумевает разработку аппарата выработки рекомендуемых к использованию значений показателей объекта мониторинга. Иначе говоря, предполагается отыскание неких нормативов, которые в дальнейшем можно было бы рекомендовать к использованию в сфере управления образованием на различных уровнях (муниципальном, региональном, федеральном). Рекомендуемые (может быть, нормативные) значения этих показателей в условиях постоянно ведущегося мониторинга должны позволить судить об отклонениях в развитии тех или иных составляющих процесса информатизации.

Можно показать, что при принятии решений по данным мониторинга образования возникает особый класс оптимизационных задач, характеризуемых специфическими ограничениями и целевой функцией, налагающих особые требования при выборе соответствующих оптимизационных алгоритмов. В частности данные задачи характеризуются большой размерностью, ограничениями специального вида, трудновычислимыми целевыми функциями.

В настоящей статье предлагается математическая модель принятия решений по данным мониторинга процессов информатизации образования в части формирования рекомендуемых значений для управляемых факторов, характеризующих процессы информатизации. Показаны специфические особенности получаемых оптимизационных моделей, выделены критерии выбора методов решения получаемых задач и представлены результаты исследований, заключающиеся в возможности применения разновидностей генетического алгоритма для их решения.

1. СПЕЦИФИКА ОПТИМИЗАЦИОННЫХ ЗАДАЧ, ВОЗНИКАЮЩИХ ПРИ ПРИНЯТИИ РЕШЕНИЙ ПО ДАННЫМ МОНИТОРИНГА ОБРАЗОВАНИЯ

1.1. Математическая постановка задачи моделирования процесса принятия решений на основе данных мониторинга

Будем называть показателем обобщенную характеристику свойств объекта мониторинга [3]. Характеристикой в нашем понимании будет признак объекта мониторинга, отражающий определенную сторону его свойств.

Например, объект любого мониторинга описывается рядом показателей, которые образованы из систем характеристик. Положим, общее число показателей N, множество индексов показателей — GN.

Характеристик, соответствующих каждому показателю, в общем случае, разное количество. Пусть Ni – число характеристик, с помощью которых количественно представляется i-й показатель объекта мониторинга, а Gi – множество индексов характеристик, образующих i-й показатель. Стоит отметить, что в общем случае некоторые характеристики могут описывать сразу несколько показателей.

Так, например, характеристика «Число компьютеров в школе в 2007 году» влияет на показатель «Динамика числа компьютеров в школе» и т.д. и «Техническое обеспечение школы». Или характеристика «Количество преподавателей в образовательных учреждениях среднего профессионального образования» оказывает влияние на показатели «Общая характеристика системы образования субъекта Федерации» и «Компетенции преподавателей в информационно-коммуникационных технологиях».

Кроме того, в терминах оптимизационных задач все характеристики объекта мониторинга суть переменные, которые можно разделить на управляемые и неуправляемые. Например, переменные «Число закупаемых компьютеров» и «Число преподавателей, направленных на повышение квалификации» — управляемые, а «Качественная успеваемость по школе» (за прошедший период) и «Число выпускников, поступивших в ВУЗ» — неуправляемые. Поэтому ниже в постановке оптимизационной задачи фигурируют только те переменные, на которые мы можем влиять.

Таким образом, имеем:

• множество характеристик (всех использующихся в конкретном обследовании)где xp – числовое значение p-й характеристики, а K – общее число уникальных характеристик (как упоминалось выше, в общем случае );
• кортеж показателей (всех использующихся в конкретном обследовании)где Xm – m-й показатель объекта мониторинга (в общем случае, значение показателей может быть как числовым, так и описательным);
• множество показателей объекта мониторинга:где xi,j – значение j-й количественной характеристики, описывающей i-й показатель (как уже говорилось выше, показатели могут иметь пересечения по некоторым характеристикам);
• пространство показателей конкретного обследования представляется как декартово произведение:

Фактически, это есть множество кортежей, состоящих из всевозможных поэлементных комбинаций характеристик каждого из показателей.

В методиках государственной статистики предусмотрено отслеживание целого ряда показателей и характеристик образования в целом и, в том числе, процессов информатизации образования [1]. Для некоторых из них сформированы в соответствии с регулирующими законодательными актами (и здравым смыслом) верхние и нижние границы, которые обозначим, соответственно, lij – минимально допустимое (нижняя граница) значение характеристики xi,j, а hij – максимально допустимое (верхняя граница).

Одним из возможных подходов к моделированию процесса принятия решений на основе данных мониторинга образования является решение оптимизационной задачи, которая сводится к отысканию таких значений характеристик объекта мониторинга xi,j,i ∈ GN, j ∈ Gi в условиях ограничений lij и hij, чтобы эффективность внедрения решения в систему образования давала максимальный эффект при ограничениях на ресурсы (возможности бюджета, сроки выполнения работ и т.д., например, невозможно повышение квалификации одновременно для 100% учителей школ).

Модель задачи в общем виде можно представит следующим образом:

(*)

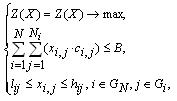где lij и hij – нижняя и верхняя границы допустимых интервальных изменений характеристики xi,j, xi,j – переменная, задающая значение характеристики объекта мониторинга номер j в показателе i, GN – множество индексов показателей объекта мониторинга, Gi – множество индексов характеристик i-го показателя объекта мониторинга, B – запасы ресурсов (например, величина бюджета), cij – издержки, связанные с изменением характеристики на единицу (например, «Покупка одного компьютера», «Повышение квалификации одного преподавателя»).

X – набор векторов значений характеристик (в общем случае разной длины), каждый из которых соответствует отдельному показателю.

 

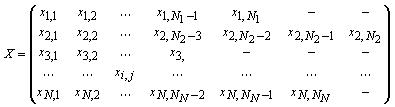
Набор векторов издержек C, связанных с изменением характеристики на единицу, идентичен по структуре набору векторов значений характеристик X.

В данной статье делаются самые общие допущения о виде целевой функции рассматриваемой задачи, в частности, предполагается, что вычисление целевой функция достаточно сложно, что требует выбора метола оптимизации с наименьшим числом обращений к процедуре ее вычисления.

1.2. Специфика оптимизационной задачи моделирования процесса принятия решений на основе данных мониторинга образования

Наш опыт проведения мониторинга информатизации и качества образования в рамках межрегионального проекта по федеральной целевой программе «Развитие единой образовательной информационной среды (2001-2005)» показал [4], что задача мониторинга образования имеет большую размерность. В пилотном мониторинге принимали участие по 30 сельских школ 6 субъектов РФ, входящих в состав Сибирского федерального округа. Мониторинг велся по 9 показателям, включающим более чем 150 характеристик, в трехгодичном временном промежутке.

Анализ существующих на сегодня подходов к решению задачи мониторинга позволил выделить ряд ее особенностей.

Например, в [5] описывается разработка системы показателей, мониторинг которых необходимо производить для достижения рассматриваемой системы целей высшей школы. Рассматривается ряд сложных, но достаточно точных, по мнению авторов, функций оценки эффективности при достижении цели. Показана сложновычислимость таких функций.

В работе [1] детально показано развитие набора показателей информатизации региональных систем образования и влияния на них в качестве регулирующих элементов законодательных актов, что ведет к появлению интервальных ограничений значений критериев мониторинга.

Авторами [6] показана линейная многопараметрическая математическая модель интегральной оценки качества образовательной системы, учитывающая взаимное влияние показателей качества, а также степень важности показателей. В работе делается упор на высокую размерность задачи.

На основании опыта проведения мониторинга, а также обзора публикаций по этой тематике были сделаны выводы о специфике задачи мониторинга:

• как правило, сложно вычислимые целевые функции;
• относительно легко вычислимые ограничения;
• высокая размерность задачи.

2. ВЫБОР И ОБОСНОВАНИЕ МЕТОДОВ ОПТИМИЗАЦИИ ДЛЯ РЕШЕНИЯ ЗАДАЧИ МОНИТОРИНГА ОБРАЗОВАНИЯ

2.1. Критерии выбора методов решения оптимизационных задач

В данной статье рассматриваются оптимизационные методы решения условных задач, основными требованиями к которым являются: сравнительно малое количество вычислений целевой функции, минимальные затраты на ее вычисление. Ведь при решении задачи вида (*), как правило, следует снижать число обращений к целевой функции в силу ее потенциальной сложности.

Формирование списка исследуемых методов осуществлялось в соответствии со следующими критериями:

• методы должны позволять решать задачи с ограничениями, как правило, легко вычислимыми;
• иметь малые вычислительные затраты;
• обеспечивать малое число обращений к целевой функции;
• позволять решать задачи больших размерностей;
• иметь приемлемую точность решения;
• иметь сравнительную легкость реализации.

Итак, на основании приведенных выше критериев в качестве исследуемых методов были выбраны следующие:

• метод Бокса (модифицированный метод Нелдера-Мида для решения условных задач);
• метод Нелдера-Мида для решения безусловных задач (условная задача сводится к безусловной с помощью метода штрафных функций).

Кроме того, для исследования были выбраны модифицированные генетические алгоритмы, рекомендованные для решения подобных задач в некоторых исследованиях [9, 10]:

• алгоритм, учитывающий ограничения при кодировании хромосом;
• генетический алгоритм решения безусловной задачи (условная задача сводится к безусловной с помощью метода штрафных функций).

Итак, перед нами стоит проблема выбора эффективного метода решения представленной выше задачи мониторинга. В качестве критериев эффективности оптимизационных методов были использованы следующие [7]:

• число обращений к целевой функции;
• машинное время вычисления;
• точность метода; для вычисления уровня отклонения вычисляемых результатов от оптимальных значений используем метрику вида длины вектора разности оптимальной точки x* и достигнутой в процессе вычисления точки :где x*i — i-ая координата известного нам заранее оптимального решения задачи, с которым сравниваем полученное в результате работы алгоритма решение .

Эксперимент проводился в две фазы. В первой в качестве критериев останова использовались рекомендованные авторами методов критерии [7, 8]. Во второй фазе критерием останова служила наихудшая точность (наибольший уровень отклонения априорного оптимального решения задачи от полученного в результате работы алгоритма C) методов, полученная в первой фазе.

2.2. Краткое описание исследуемых методов для решения задачи оптимизации

Метод штрафных функций используется для преобразования исходной задачи условной оптимизации в последовательность задач безусловной оптимизации, решаемых конкретным методом.

При использовании методов штрафных функций получается максимальный оптимизирующий эффект за счет компромисса между необходимостью удовлетворения ограничений и процессом минимизации целевой функции. Это становится возможным благодаря взвешиванию целевой функции и функций, задающих ограничения [7]. Влияние входящих в штрафную функцию ограничений в процессе оптимизации с увеличением числа итераций ослабевает, а в пределе полностью исчезает. В результате последовательность промежуточных значений штрафной функции сходится к тому же значению, что и последовательность значений целевой функции. Таким образом, их экстремумы совпадают.

Для того, чтобы в оптимизационных задачах (*) можно было использовать целевую функцию самого различного вида, в том числе, алгоритмически вычисляемую, очевидно, более целесообразно использовать алгоритмы оптимизации, не предусматривающие процедуры дифференцирования данной функции.

Поэтому при формировании штрафной функции мы можем использовать штраф любого вида, в том числе получаемый при помощи недифференцируемой функции, как показано ниже.

Итак, функция штрафа для ограничений типа неравенство имеет вид:

 

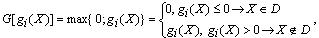
где gi(X)i, i ∈ Iн — i-я функция-ограничение типа неравенство; где Iн – множество индексов функций-ограничений типа неравенство.

Функция штрафа для ограничений типа равенство:

 

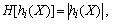
где hi(X)i, i ∈ Ip — i-я функция-ограничение типа равенство; Ip — множество индексов функций-ограничений типа равенство.

Метод Нелдера-Мида используется для решения безусловной задачи, которая получается путем преобразования условной задачи при помощи метода штрафных функций.

Далее метод будем называть для краткости «метод Нелдера-Мида для оптимизации штрафной функции».

Метод Нелдера-Мида имеет также название «метод деформируемого многогранника» и является весьма эффективным и легко реализуемым программно [7]. Деформируемый многогранник характеризуется способностью легко адаптироваться к топологии задачи, в том числе для функций типа «овражных», что ускоряет процесс решения.

Метод Бокса (модифицированный метод Нелдера-Мида для решения задач с ограничениями) — метод комплексов, предложенный Боксом, — характеризуется сравнительной простотой реализации и невысокими требования к объему памяти вычислительной машины [8]. Этот метод является одним из наиболее быстрых не градиентных методов многомерной условной оптимизации.

Генетический алгоритм с кодированием ограничений. Как известно, генетические алгоритмы применяются для решения оптимизационных задач с помощью метода эволюции, то есть путем отбора из множества решений наиболее подходящего. Генетические алгоритмы характеризуются способностью решать некоторые типы задач, с которыми традиционные методы не справляются. Например, такие задачи, для которых вычислительные сложности растут экспоненциально с размерностью задачи, а также комбинаторные задачи и задачи, математическое описание которых не является гладкой непрерывной функцией.

Здесь рассматривается алгоритм, существенным отличием которого от классического подхода к схеме генетического алгоритма [9, 10] является использование ограничений в декодировании хромосом, что позволяет исключить этап отсеивания решений, не попадающих в область допустимых значений.

Генетический алгоритм для решения безусловной задачи (условная задача при этом сводится к безусловной с помощью метода штрафных функций). Далее будем называть для краткости «генетический алгоритм для оптимизации штрафной функции».

В рассматриваемом алгоритме последовательность безусловных задач, полученная при преобразовании условной оптимизационной задачи, решается при помощи генетического алгоритма. Можно сказать, что это схема решения задачи, в которой на каждой итерации оптимальное решение вновь сгенерированной штрафной функции находится с помощью генетического алгоритма (рис. 1).

 

 

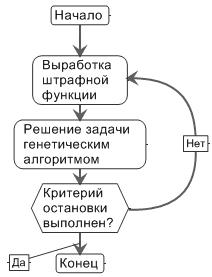
Рис. 1. Общая схема работы генетического алгоритм для оптимизации штрафной функции

2.3. Формирование тестовых задач для исследования оптимизационных методов

Рассмотрим, как ведет себя реальная задача оптимизации с разными параметрами и разной размерностью. Для исследования алгоритмов был разработан ряд тестовых, достаточно простых, задач, имеющих некоторым образом сходную с задачей мониторинга специфику. Для этих задач заранее известно как поведение, так и оптимальное решение. В качестве тестовых задач было решено использовать следующие.

1. Для выяснения поведения методов на задачах с малой размерностью использовались следующие задачи размерностью 2:
2. Для задач с размерностью больше 2:

Для исследования поведения методов на задачах с овражной целевой функцией используются задачи 1.Б. и 2.Б. Известно, что для таких задач наблюдается плохая сходимость в смысле скорости в силу многократного увеличения степени влияния отдельных переменных на значение целевой функции [8].

Для рассматриваемых задач был принят следующий вид штрафной функции:

• для варианта задачи, размерностью 2
• для варианта задачи размерностью больше 2 где α — штрафной параметр функций-ограничений неравенства.

2.4. Особенности реализации программных модулей

В силу специфики задачи, моделирующей процессы принятия решений на основе данных мониторинга образования, использование существующих программных пакетов не всегда эффективно для исследования предлагаемых методов оптимизации. Поэтому для реализации и исследования описанных методов оптимизации были разработаны программные модули поиска экстремума функции, основанные на вышеперечисленных алгоритмах. В качестве средства реализации выбран язык C++.

Модули являются узкоспециализированными, предназначенными для исследования описанного выше типа задач. Они были объединены в один исследовательский программный пакет, что позволило провести их совместное исследование.

Модуль «Метод Бокса» и модуль «Метод Нелдера-Мида для оптимизации штрафной функции» не представляют сложности в реализации, в связи с чем их подробное описание здесь не приводится.

Основные особенности модуля «Генетический алгоритм с кодированием ограничений», алгоритм которого изложен в работе [9], заключаются в использовании ограничений в кодировании хромосом, в результате чего все генерируемые решения заранее лежат в допустимой области, а также в отсутствии таких этапов классического генетического алгоритма, как расширение популяции за счёт новых особей и сокращение популяции до исходного размера. Последнее объясняется тем, что происходит взаимный обмен генами между материнской и отцовской хромосомами, то есть новое поколение – это видоизменённые родители.

Программный модуль «Генетический алгоритм для оптимизации штрафной функции» реализует, по сути, классический алгоритм, однако имеет ряд особенностей, описанных ниже.

Алгоритм работы программы показан на рисунке 2.

Генерация начальной популяции происходит по заданным ограничениям в пространстве параметров.

Отбор пар производится по техникам инбридинга или аутбридинга [9, 10] (в пару выбираются особи с наименьшим или наибольшим взаимным расстоянием (Хемминговым или разности координат) соответственно).

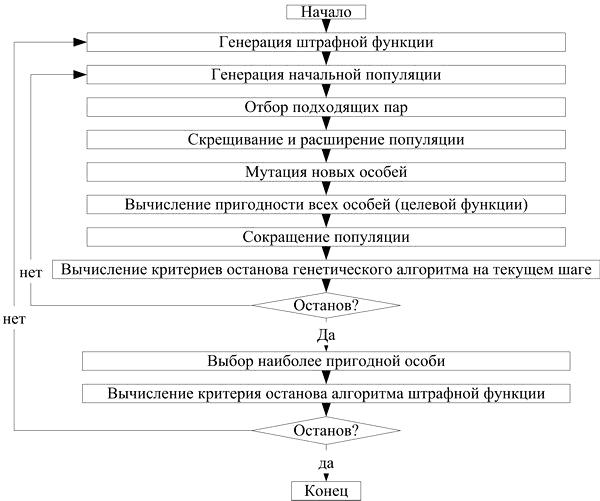
Рис. 2. Схема алгоритма работы программы

Кроссовер (скрещивание) предусмотрен четырех типов. Одноточечный и двухточечный кроссовер реализованы полностью по классической схеме. Случайный кроссовер случайным образом выбирает одно- или двухточечный кроссовер. Модифицированный равномерный кроссовер работает по схеме одноточечного кроссовера для каждой координаты с возможностью обмена. Алгоритм модифицированного равномерного кроссовера приведен ниже (рис. 3).

 

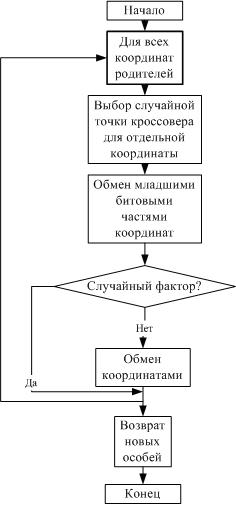
Рис. 3. Алгоритм модифицированного равномерного кроссовера

С некоторой вероятностью алгоритм для каждой координаты хромосомы выбирает набор генов из брачных пар и с некоторой, но уже другой вероятностью проводит одноточечный обмен всего выбранного набора генов (рис. 4). Было решено не реализовывать равномерный кроссовер в чистом виде ввиду его чрезмерной трудоемкости и того, что модифицированный равномерный кроссовер показывает приемлемые результаты, особенно в сочетании с кодом Грея и аутбридингом алгоритма [10].

 

 

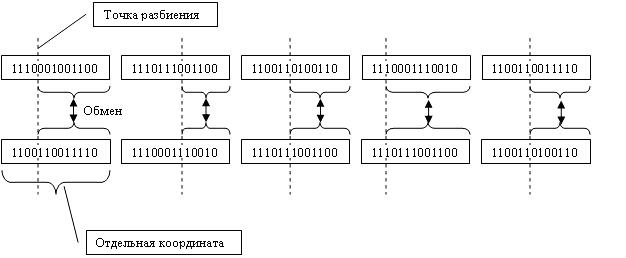
Рис. 4. Пример работы модифицированного равномерного кроссовера

Мутации происходят либо по классической схеме, либо по модифицированной схеме. Классическая схема («множественные мутации») подразумевает мутирование каждого бита в хромосоме в зависимости от вероятности мутации. Для этой схемы вероятность мутаций должна быть достаточно мала. Модифицированная схема подразумевает мутацию одного случайного бита в хромосоме с заданной вероятностью. Для этой схемы вероятность должна быть велика.

Для сокращения шанса мутации или обмена незначащими цифрами координат, в программу введено понятие битового максимума. Он представляет собой максимальное число значащих битов в наибольшем значении ограничения в пространстве параметров. Он используется в алгоритмах кроссовера и мутаций для ограничения номера бита, который использован в качестве мутируемого или в качестве точки разрыва.

2.5. Результаты тестирования

С использованием разработанных программных модулей были проведены исследования поведения тестовой задачи с целью оценить, какой метод наиболее подходит для решения задач указанной специфики.

Работа всех программных модулей находилась в одинаковых условиях:

• все программы выполнялись в системе с конфигурацией Intel Pentium IV Celeron 1.7 ГГц, 512 Мб ОЗУ, ОС Windows XP Professional;
• для всех модулей использовались общие ограничения, содержащиеся в отдельном, заранее сгенерированном файле.

Метод Бокса (модифицированный метод Нелдера-Мида)

В результате проведенного исследования метода комплексов Бокса (основные результаты представлены в таблицах 1-4) были выявлены условия использования метода:

• функция с относительно небольшим числом переменных (не более 100);
• легко вычислимая целевая функция.

При следовании этим рекомендациям соответственно возрастет скорость сходимости метода и его точность.

Метод Нелдера-Мида для оптимизации штрафной функции

При исследовании метода Нелдера-Мида для оптимизации штрафной функции тестирование показало, что метод плохо работает уже на небольших размерностях (таблицы 1-4).

Генетический алгоритм с кодированием ограничений

Исследования работы алгоритма показали, что он хорошо работает на малых размерностях, при увеличении же размерности задачи точность алгоритма резко уменьшается. В ходе тестирования были выявлены параметры, которые в большей степени влияют на сходимость алгоритма для обычных и овражных функций, и определены предпочтительные значения этих параметров. Кроме того, результаты показали, что с овражными функциями алгоритм работает не очень хорошо. Это надо будет учитывать при построении реальной целевой функции.

Результаты эксперимента представлены в таблицах 1-4.

Генетический алгоритм для оптимизации штрафной функции

Было отмечено, что при увеличении точности время вычисления и количество вычислений целевой функции значительно увеличивается, что имеет критическое значение при работе программы на компьютере с невысокой производительностью.

В целом же результаты исследования показали, что генетический алгоритм со штрафной функцией наиболее приемлемый алгоритм для решения задачи (*).

Результаты тестирования приведены в таблицах 1-4.

Стоит отметить, что для задач размерностью больше 100 при увеличении заданного максимума поколений до значения, большего исходного размера популяции можно добиться лучшей сходимости. Однако в этом случае резко возрастает время вычисления.

В ходе исследований алгоритм был доработан путем ввода дополнительных генетических операторов, таких, как различные виды мутации, скрещивания и кодирования.

Сводные таблицы результатов экспериментов

Таблица 1. Результаты исследования методов на тестовых задачах размерностью 2

	Размерность	2
	Метод	Метод Бокса (модифицированный Нелдера-Мида)	Метод Нелдера-Мида для оптимизации штрафной функции		Генетический алгоритм с учетом ограничений в кодировании хромосом	Генетический алгоритм для оптимизации штрафной функции
Номер задачи	Параметры →	P = 2n,α = 1,31	Случайное начальное приближение	Оптимальное начальное приближение2	K = 1203Ps = 0.5	Кодирование в прямом коде,M = 504
	Критерии качества алгоритма ↓
1А	Число вычислений ЦФ5	2	107	8	567	3
	Время вычисления (с)	6,17*10-4	0,477	0,06	0,131	4,87*10-6
	Точность (критерий останова)	0,8636
1Б	Число вычислений ЦФ	8	132	90	567	119
	Время вычисления (с)	3,59*10-3	0,795	0,643	0,121	1,97*10-3
	Точность (критерий останова)	0,863

Таблица 2. Результаты исследования методов на тестовых задачах размерностью 10

	Размерность	10
	Метод	Метод Бокса (модифицированный Нелдера-Мида)	Метод Нелдера-Мида для оптимизации штрафной функции	Генетический алгоритм с учетом ограничений в кодировании хромосом	Генетический алгоритм для оптимизации штрафной функции
Номер задачи	Параметры →	P = 2n,α = 1,3	Оптимальное начальное приближение	K = 120Ps = 0.5	Кодирование в прямом коде,M = 50
	Критерии качества алгоритма ↓
2А	Число вычислений ЦФ	30	78	1039	143
	Время вычисления (с)	0,021	0,055	6,9	0,0038
	Точность (критерий останова)	0,586
2Б	Число вычислений ЦФ	168	5190	2155	538
	Время вычисления (с)	0,3379	8,017	16,09	0,029
	Точность (критерий останова)	0,4175

Таблица 3. Результаты исследования методов на тестовых задачах размерностью 100

	Размерность	100
	Метод	Метод Бокса (модифицированный Нелдера-Мида)	Метод Нелдера-Мида для оптимизации штрафной функции	Генетический алгоритм с учетом ограничений в кодировании хромосом	Генетический алгоритм для оптимизации штрафной функции
Номер задачи	Параметры →	P = 2n,α = 1,3	Оптимальное начальное приближение	K = 120Ps = 0.5	Кодирование в прямом коде,M = 50
	Критерии качества алгоритма ↓
2А	Число вычислений ЦФ	4373	3,83*104	4870	1280
	Время вычисления (с)	8,4187	52,4393	247,232	1,386
	Точность (критерий останова)	0,744
2Б	Число вычислений ЦФ	9,37*104	17,009*104	3017	1034
	Время вычисления (с)	173,047	167,197	97,3124	53,4
	Точность (критерий останова)	2,11

Таблица 4. Результаты исследования методов на тестовых задачах размерностью 1000

	Размерность	1000
	Метод	Метод Бокса (модифицированный Нелдера-Мида)	Метод Нелдера-Мида для оптимизации штрафной функции	Генетический алгоритм с учетом ограничений в кодировании хромосом	Генетический алгоритм для оптимизации штрафной функции
Номер задачи	Параметры →	P = 2n,α = 1,3	Оптимальное начальное приближение	K = 120Ps = 0.5	Кодирование в прямом коде,M = 50
	Критерии качества алгоритма ↓
2А	Число вычислений ЦФ	3,067*106	16,582*106	5036	3279
	Время вычисления (с)	48,8829	232,23	760,34	53,201
	Точность (критерий останова)	4,28
2Б	Число вычислений ЦФ	90,762*106	156,83*106	5969	3232
	Время вычисления (с)	1403,832	2907,94	737,9063	287,3434
	Точность (критерий останова)	5,41

Сводные графики для задачи 2.Б. размерностью 1000 (наибольшая размерность в эксперименте, приближенная к реальной задаче) представлены на рис. 5 и 6.

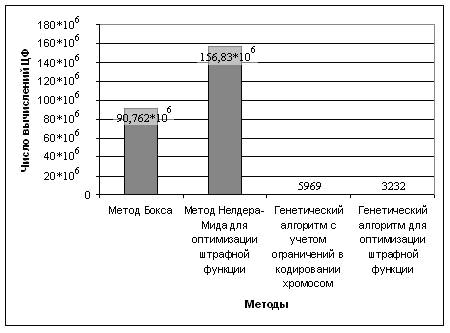
Рис. 5. Число вычислений целевой